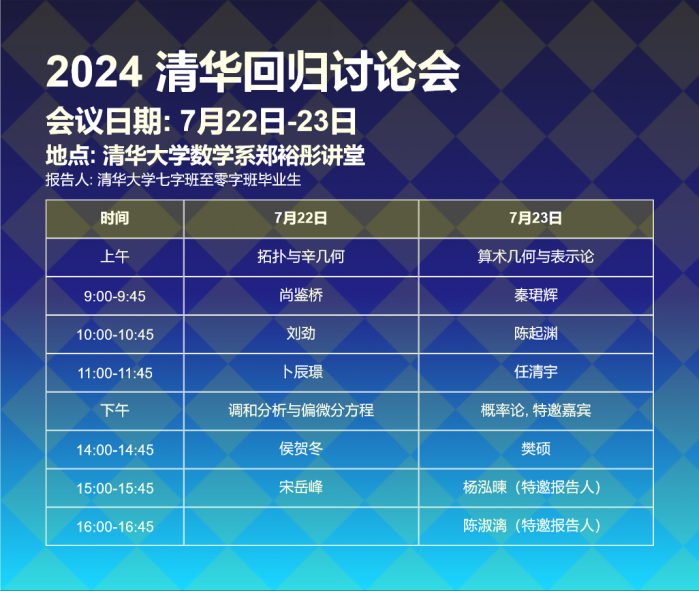
7月22日—23日,清华数学科学系优秀校友将重聚母校,一同分享他们毕业以来在数学方面的工作与见解。
会议日期: 7月22日-23日
地点: 清华大学数学科学系郑裕彤讲堂
7月22日上午: 拓扑与辛几何
9:00-9:45: 尚鉴桥
10:00-10:45: 刘劲
11:00-11:45: 卜辰璟
下午: 调和分析与偏微分方程
14:00-14:45: 侯贺冬
15:00-15:45: 宋岳峰
7月23日上午: 算术几何与表示论
9:00-9:45: 秦珺辉
10:00-10:45: 陈起渊
11:00-11:45: 任清宇
下午: 概率论, 特邀嘉宾
14:00-14:45: 樊硕
15:00-15:45: 杨泓暕(特邀报告人)
16:00-16:45: 陈淑漓(特邀报告人)
尚鉴桥 (Université Paris-Saclay)
标题:一个Morse同调的引理
摘要:(引理)考虑流形M与紧子流形N,以及M上的Morse函数f。如果f在M和N上拥有相同的奇异点与指标,那么M与N的Morse同调相同。
我们将证明该引理,用其解释Lagrange乘子法的Morse理论, Viterbo同构等定理为何正确。之后我们会从其出发,解释进一步对辛同调能猜想什么。
刘劲 (Université Grenoble Alpes)
标题:内接方形问题
摘要:对于平面上的简单闭曲线,是否总有一个正方形,它的四个顶点都在这条曲线上?这是一个有超过一百年历史的问题,对于很多类型的曲线得到了证明,但一般情形依然是未知的。
近几年来,通过引入来自辛几何的想法,Joshua Greene和Andrew Lobb取得了一些重要突破。
我们将介绍问题的历史以及进展。简述Greene和Lobb创建的Jordan Floer homology理论及在此问题上的应用。
卜辰璟 (University of Oxford)
标题:顶点代数与同调
摘要:顶点代数是一种源于共形场论的代数结构。我们介绍顶点代数与拓扑空间的同调之间的一个神秘联系,即某些空间的同调带有顶点代数的结构。利用此结构,我们将某些模空间的基本类写成一个发散的无穷求和,这能给出计算模空间上相交数的新公式。这些结论的物理意义仍有待探索。
侯贺冬 (Université Paris-Saclay)
标题: Well-posedness for parabolic Cauchy problems with distributional initial data.
摘要: Used by Koch--Tataru for Navier--Stokes equations, the theory of tent spaces turns out to be useful to deal with evolution equations allowing distributional initial data, due to its strong connection with harmonic analysis as shown in the eminent works of Fefferman--Stein and Coifman--Meyer--Stein. In this talk, we use tent spaces to investigate well-posedness of Cauchy problems of linear parabolic equations with time-independent, uniformly elliptic, bounded measurable complex coefficients, with various possible sorts of source terms. The initial data can be tempered distributions taken in homogeneous Hardy-Sobolev spaces \dot{H}^{s,p} with -1<s<1. The talk is based on a series of joint works with Pascal Auscher.
宋岳峰 (Stanford University)
标题:Einstein-Euler系统的弱零奇点
摘要:We study the behavior of a self-gravitating perfect relativistic fluid satisfying the Einstein–Euler system in the presence of a weak null terminal spacetime singularity. This type of singularities is expected in the interior of generic dynamical black holes. In the vacuum case, this type of singularities has been constructed locally by Luk, where the metrics extend continuously to the singularities while the Christoffel symbols fail to be square integrable in a neighborhood of any point on the singular boundaries. We prove that this type of singularities persists in the presence of a self-gravitating fluid. Moreover, using the fact that the speed of the fluid is strictly less than the speed of light, we prove that the fluid variables also extend continuously to the singularity.
标题: Around de Rham stack
摘要: We start by reviewing the history of (algebraic) de Rham stack, with an emphasis on the work of Gaitsgory--Rozenblyum. Then we talk about the recent work of Rodríguez Camargo on analytic de Rham stack, and show the connection with some early work of Große-Klönne on overconvergent de Rham cohomology.
樊硕 (Tsinghua University and IHES)
标题:Quasi-invariance of SLE welding
摘要:When κ∈(0,4], the SLE loop η_κ is an important one-parameter family of conformally invariant and conformally removable random Jordan loops with Hausdorff dimension 1+κ/8. We study the conformal welding of this loop and prove that this random welding measure is mutually absolutely continuous with itself under post-composition and pre-composition by Weil--Petersson quasi-symmetric homeomorphisms, what we call quasi-invariance. In particular, the new welding question still has a unique solution with the same Hausdorff dimension. Weil--Petersson geometry theory of the universal Teichmüller space is an important topic in Teichmüller theory, which is closely related with Loewner energy that also appears in the large deviation principle of SLE. Our result shows the interplay between probability theory and geometry. For the proof, we use the tool from Liouville quantum gravity, more precisely, the normalized boundary Liouville measure which is also quasi-invariant. Moreover, we find some other random conformal welding measures are also quasi-invariant.
特邀报告人 杨泓暕 (Stanford University)
标题: Instantons and Khovanov homology in RP^3
摘要: Following Kronheimer and Mrowka’s approach, we show that Khovanov homology detects the unknot and the projective unknot in RP^3. I’ll explain the idea of the proof. Time permitting, I’ll discuss potential further detection results.
特邀报告人 陈淑漓 (Stanford University)
标题: Positive scalar curvature metrics and aspherical summands
摘要: A closed manifold is called aspherical if it has contractible universal cover. It has been conjectured since the 80s that all closed aspherical manifolds do not admit metrics with positive scalar curvature. In dimensions 3,4,5 this conjecture is solved by works of Gromov—Lawson, Chodosh—Li, Gromov, and Chodosh—Li—Liokumovich. We prove for n = 3,4,5 that the connected sum of a closed aspherical n-manifold with an arbitrary manifold does not admit a complete metric with nonnegative scalar curvature. More generally, we generalize the partial classification result of Chodosh, Li, and Liokumovich to the non-compact domination case with our newly-developed technique. This is joint work with Jianchun Chu (Peking University) and Jintian Zhu (Westlake University).
会议海报
特别鸣谢:新基石科学基金会
